Encoding gravity - without gravity
1 August 2019
There has recently been a major shift in the way physicists think about quantum gravity – the combined theory of quantum mechanics and gravity. This shift arose from the discovery that a wide range of purely quantum-mechanical systems, with no gravity present, are secretly described by the same mathematics as theories of quantum mechanics and gravity. It is as if the same rule book is used to describe two entirely different games – although a better analogy is probably that of a cryptogram with an encoded message, as it is not always easy to translate results from one system to the other.
Encoding and decoding
Yet, one can tease out the hidden quantum gravity theory by carefully studying how information is encoded in the purely quantum-mechanical system. It is particularly interesting to ask how natural objects in the theory of quantum gravity – black holes, for example – can be translated into the language of the purely quantum-mechanical theory.
In a paper that was published in Physical Review X this week, UvA physicist Michael Walter together with five colleagues from Stanford, Caltech, Harvard, and Brandeis provides a mathematical construction for this translation. Using tools that were originally developed to handle noise in quantum information processing, they construct a ‘communication channel’ that takes as input objects on the quantum gravity side and outputs corresponding objects on the purely quantum-mechanical side.
Redundance and recovery
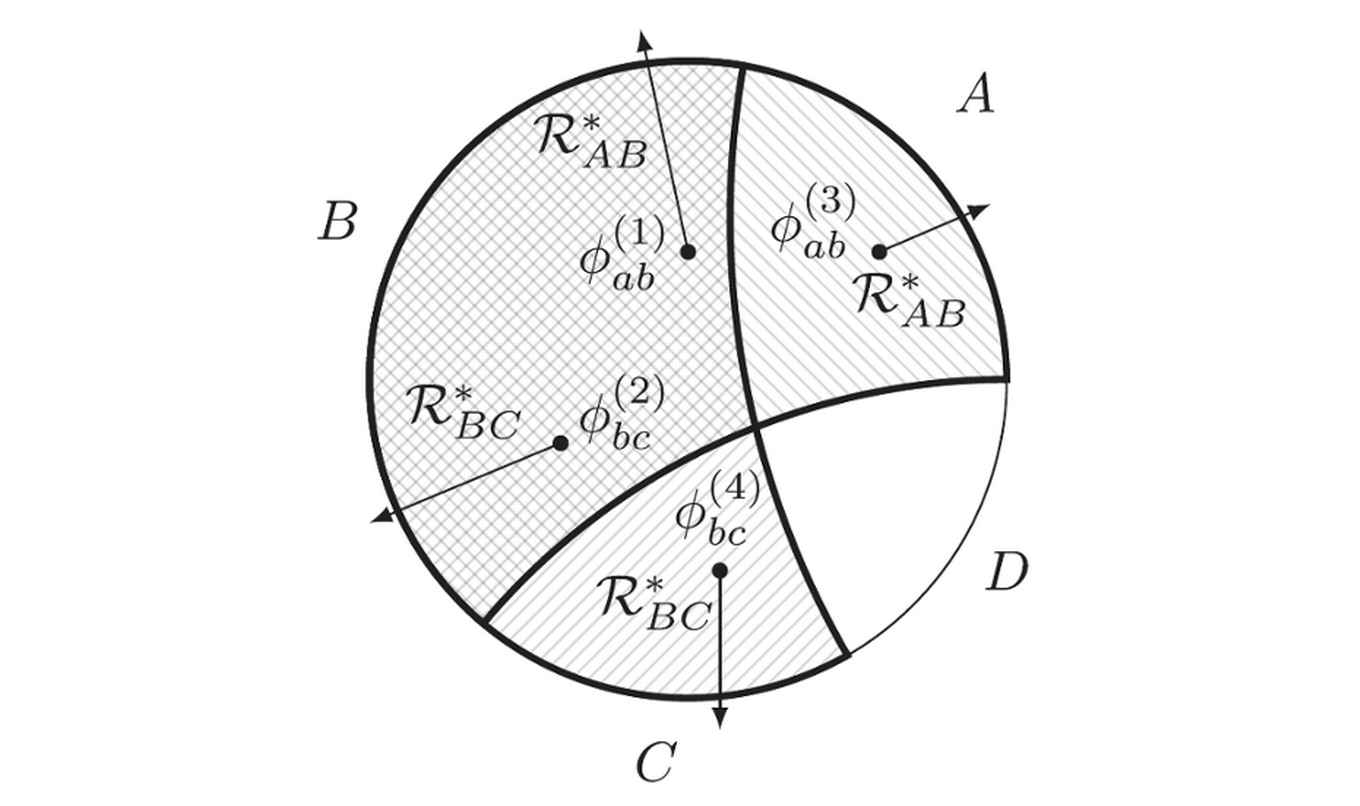
A unique challenge for this translation protocol is that quantum-gravitational objects are redundantly encoded in the purely quantum mechanical system. That is: even if part of the quantum mechanical theory is erased, the encoded gravitational objects may still be recovered. The authors construct a ‘recovery mapping’ that explains how to recover quantum-gravitational information when some of its redundant description is erased. Since the ability to translate between different yet equivalent descriptions of quantum-gravitational objects lies at the heart of many of the latest developments in quantum gravity research, this new ‘communication channel’ may prove to be a useful tool for future research on this intriguing topic.
Reference
Jordan Cotler, Patrick Hayden, Geoffrey Penington, Grant Salton, Brian Swingle, and Michael Walter, Entanglement Wedge Reconstruction via Universal Recovery Channels, Phys. Rev. X 9, 031011.